Лекция 2.Раздел 2.1
Скалярное произведение

Кроме указанных выше операций сложения векторов и умножения вектора на число существуют и другие операции. Рассмотрим, например, задачу о вычислении работы под воздействием постоянной силы на прямолинейном участке пути. Как известно, она равна произведению силы на путь, то есть  . При этом обе входящие в произведение величины являются векторами.

Определение. Скалярным произведением векторов   и   называется произведение их длин на косинус угла между ними.

Обозначается скалярное произведение следующим образом:

        (2.1.1)

где   – угол между и   . Отсюда получаем известную формулу для работы:

       (2.1.2)

Основными свойствами скалярного произведения являются:

1. перестановочное
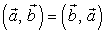
2. сочетательное
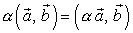
3. распределительное
4. 

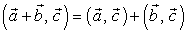
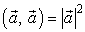
Теорема 2.1.1. Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны.

Доказательство. Рассмотрим скалярное произведение  . Пусть  . При вычислении скалярного произведения рассматриваются вектора, длина которых не равна нулю. Следовательно, это произведение может быть равно нулю лишь при условии, что равен нулю третий сомножитель. Таким образом,   и  , что и требовалось доказать.

Рассмотрим обратное утверждение: , отсюда  . Но тогда  и  , что и требовалось доказать.

Из выражения для скалярного произведения следуют некоторые полезные формулы. Если рассмотреть вектора    и   , то, очевидно, что . Значит, из выражения следует, что

и 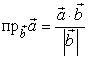       (2.1.3)

Кроме того, угол между векторами также можно определить из скалярного произведения:

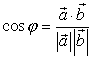       (2.1.4)

Теорема 2.1.2. В ортонормированном базисе скалярное произведение равно:

       (2.1.5)

Доказательство. Вычислим:

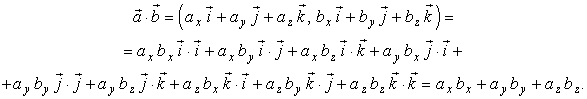
Пользуясь этим правилом, получаем:

откуда