Ответ к задаче 37
Для каждого уже записанного числа A вы дописываете число, цифры которого получаются как дополнения до 9 соответствующих цифр числа A.
Если были записаны m чисел, состоящих из n цифр, то сумма этих m чисел и чисел, записанных вами согласно вышеописанному правилу будет равна 10n·m – m.
Если среди первоначально записанных чисел есть число вида 99...9, тогда для него не нужно писать дополнительное число.
Обоснование.
- Если записано число из (n+1) цифр
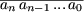 an≠0,
и вы дописываете число
an≠0,
и вы дописываете число
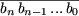 , где bi=9–ai i=0, 1, ..., n,
, где bi=9–ai i=0, 1, ..., n,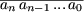 и
и
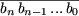 будет равна
будет равна
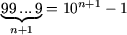 .
.
- Если an=9 и an-1≠9, тогда вы дописываете число
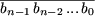 , где bi=9–ai i=0, 1, ..., n-1,
, где bi=9–ai i=0, 1, ..., n-1,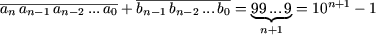 .
.
Обратно к задачам
