Лекция 15. Раздел 15.4
Асимптоты функции.

В предыдущих пунктах были рассмотрены методы исследования поведения функции с помощью производной. Однако среди вопросов, касающихся полного исследования функции, есть и такие, которые с производной не связаны.

Так, например, необходимо знать, как ведет себя функция при бесконечном удалении точки ее графика от начала координат. Такая проблема может возникнуть в двух случаях: когда аргумент функции уходит на бесконечность и когда при разрыве второго рода в конечной точке уходит на бесконечность сама функция. В обоих этих случаях может возникнуть ситуация, когда функция будет стремиться к некоторой прямой, называемой ее асимптотой.

Определение. Асимптотой графика функции называется прямая линия, обладающая тем свойством, что расстояние от графика до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Различают два типа асимптот: вертикальные и наклонные.

К вертикальным асимптотам относятся прямые линии , которые обладают тем свойством, что график функции в их окрестности уходит на бесконечность, то есть, выполняется условие: . Очевидно, что здесь удовлетворяется требование указанного определения: расстояние от графика кривой до прямой стремится к нулю, а сама кривая при этом уходит на бесконечность. С таким поведением функций мы сталкивались в п. 11.1, когда речь шла о разрывах второго рода. Итак, в точках разрыва второго рода функции имеют вертикальные асимптоты, например, в точке . Следовательно, определение вертикальных асимптот функции совпадает с нахождением точек разрыва второго рода.

Наклонные асимптоты описываются общим уравнением прямой линии на плоскости, то есть . Значит, в отличие от вертикальных асимптот, здесь необходимо определить числа и .

Итак, пусть кривая имеет наклонную асимптоту, то есть при точки кривой сколь угодно близко подходят к прямой (рис. 15.4.1). Пусть – точка, расположенная на кривой. Ее расстояние от асимптоты будет характеризоваться длиной перпендикуляра . Согласно определению, . Но вычисляется довольно сложно, гораздо проще найти .

Из треугольника следует, что , так как . Значит, . Итак, .

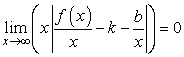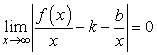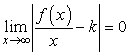Но выше было сказано, что , откуда следует, что . Вынесем в данном выражении за скобки: . Так как по условию , то . Здесь , следовательно, , откуда получаем: .

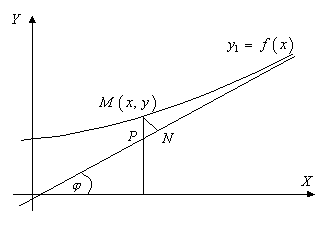
Рис. 15.4.1

Зная , рассмотрим снова предел: . Он выполняется лишь при условии, что

.

Таким образом, найдены и , а с ними и уравнение наклонной асимптоты. Если , то получаем частный случай горизонтальной асимптоты . При невозможности найти хотя бы один предел (при вычислении или ) делается вывод, что наклонной асимптоты нет.

Аналогично проводится исследование и при .