Лекция 4. Раздел 4.3
Параметрическое и каноническое уравнение прямой.

Чтобы задать прямую, необходимо задать две точки или одну точку и направление прямой. Пусть прямая проходит через точку параллельно вектору . Точка при этом называется начальной, а вектор – направляющим. Поместим прямую в прямоугольную декартовую систему координат, то есть каждой точке прямой поставим в соответствие радиус-вектор (рис. 4.3.1).

Рис. 4.3.1

Точка имеет радиус-вектор . Возьмем произвольную точку на прямой, ее радиус-вектор . Чтобы вектор был параллелен вектору , необходимо, чтобы , где . Число называется параметром, а само уравнение – векторным параметрическим уравнением прямой.

Разлагая векторы этого уравнения по базису, получим три или два скалярных уравнения:

Это и есть параметрическое уравнение прямой.

Исключим параметр из этого уравнения: ; ; .

Полученное уравнение называется каноническим уравнением прямой. В знаменателе его стоят компоненты направляющего вектора.

На плоскости каноническое уравнение прямой имеет вид:

.

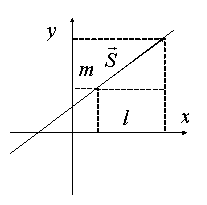
Рис. 4.3.2

Из рис. 4.3.2 видно, что в уравнении прямой линии – угловой коэффициент, – отрезок, отсекаемый прямой от оси .

Если взять две ортогональных прямых на плоскости (рис. 4.3.3), то

.

Значит, угловые коэффициенты взаимно перпендикулярных прямых связаны между собой.

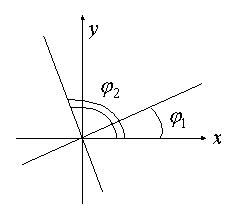
Рис. 4.3.3