Лекция 11. Раздел 11.2
Производная функции одной переменной.

Рассмотрим задачу о прямолинейном движении тела с переменной скоростью. Это может быть свободным падением тела, движением поршня в цилиндре и т.д.

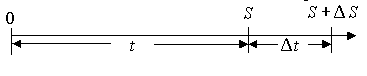
Рис. 11.2.1

Пусть в момент времени тело находилось на расстоянии от начала своего движения. Как только время изменится на величину , тело переместится из положения в . Значит, пройденный телом путь за время изменится на (рис. 11.2.1).

Чтобы найти среднюю скорость на этом отрезке, необходимо разделить путь на время, то есть . Но эта скорость не характеризует точно сам процесс движения. Поэтому стремятся уменьшить период для повышения точности в определении скорости. В пределе, когда , получают мгновенную скорость, то есть или .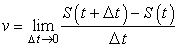

Так, при свободном падении тела, пройденный им за время путь равен . Возьмем новый момент времени . Тогда 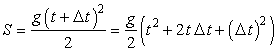. Отсюда , значит, и , то есть, получено известное из физики выражение.

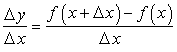Рассмотрим теперь произвольную функцию , непрерывную на отрезке . Если ее аргумент приобретает некоторое приращение , то изменяется и сама функция, при этом . Составим отношение и найдем его предел, когда .

Определение 11.2.1. Если существует предел отношения приращения функции к приращению ее аргумента , когда , то этот предел называется производной данной функции и обозначается .

Процесс вычисления производной называется дифференцированием функции.

Выясним геометрический смысл производной. Для этого рассмотрим график функции (рис. 11.2.2). Пусть фиксированная точка этой кривой, а – меняющая свое положение. Проведем через и хорду. Тогда, по мере приближения к , хорда превращается в касательную линию к графику функции в точке . Хорда образует с положительным направлением оси угол , который можно найти из выражения . По мере приближения к величина угла стремится к величине угла , который образует с осью касательная к кривой в точке . Значит,

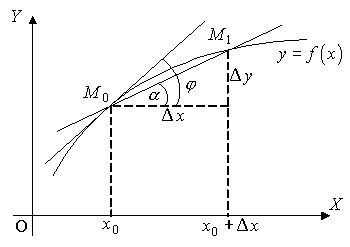
Рис. 11.2.2

Теорема 11.2.1. С геометрической точки зрения производная функции в точке равна тангенсу угла, который образует касательная, проведенная к графику данной функции в точке , с положительным направлением оси .

Определение 11.2.2. Если функция имеет производную в точке , говорят, что она дифференцируема в этой точке. Если функция имеет производную в каждой точке отрезка , говорят, что она дифференцируема на отрезке.

Между дифференцируемостью функции и ее непрерывностью существует прямая связь.

Теорема 11.2.2. Если функция имеет производную в точке , то она непрерывна в этой точке и некоторой ее окрестности.

Доказательство. Так как , то на основании теоремы 9.2.1 можно записать: , где – бесконечно малая величина. Тогда . Но согласно определению 11.1.1 данная функция непрерывна, что и требовалось доказать.

Обратное утверждение несправедливо. Действительно, функция непрерывна, но при производной не имеет.