Лекция 6. Раздел 6.5
Теорема Кронекера - Капелли.

Как было сказано в разделе 6.4, существуют совместные и несовместные системы линейных алгебраических уравнений. Поэтому, прежде чем перейти к вопросу о методах решения этих систем, рассмотрим теорему, позволяющую определять, имеют или не имеют они решение.

Теорема Кронекера - Капелли. Для совместности системы линейных алгебраических уравнений необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу ее расширенной матрицы.

Докажем необходимость. Дано, что система совместна, то есть существует совокупность чисел , которая обращает ее уравнения в тождество. Значит,

.

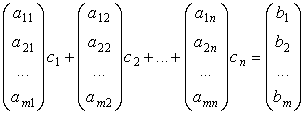Отсюда следует, что столбец свободных членов является линейной комбинацией столбцов из коэффициентов системы. Значит, это же можно сказать и о последнем столбце расширенной матрицы. Но если последний столбец расширенной матрицы является линейной комбинацией остальных столбцов, то согласно теореме о базисном миноре он не может быть базисным. Следовательно, все базисные, то есть линейно независимые столбцы, расположены в основной матрице системы. Отсюда, , что и требовалось доказать.

Докажем достаточность. Дано, что . Тогда существует минор , являющийся базисным одновременно и у и у . В этом случае он должен содержать одни и те же столбцы. Очевидно, что последний столбец расширенной матрицы, в этом случае, входить в базисный минор не может. Согласно теореме о базисном миноре, столбцы, не входящие в него, могут быть представлены в виде линейной комбинации базисных. Значит, существуют такие числа , что

.

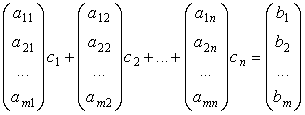Но это запись линейной системы алгебраических уравнений, в которой неизвестные заменены решением, то есть система совместна, что и требовалось доказать.