Лекция 8. Раздел 8.2
Отображения и функции.

Из практики известно, что существует множество задач, в которых значение одной величины определяет значение другой. Так, например, площадь квадрата зависит от длины его стороны, путь, пройденный автомобилем при равномерном движении, – от времени движения и т.д. Следовательно, задавая множество значений одной величины и зная ее связь с другой, мы всегда с точностью можем назвать множество значений другой величины. Абстрагируясь от конкретных задач и изучая только лишь свойства таких взаимосвязей, математика пришла к понятию функции.

Определение 8.2.1. Если между двумя множествами X и Y существует такое отношение, что для поставлен в соответствие один и только один элемент , то говорят, что задано функциональное соотношение f между X и Y.

Множество называется областью определения функции и обозначается , множество называется множеством значений функции и обозначается , пи этом называется независимой переменной или аргументом функции, а зависимой переменной или значением функции. Обычно функция обозначается с помощью записи .

Если множество отображается в , каждый элемент имеет одно и только одно изображение . Однако не обязательно, чтобы каждый элемент из был изображением какого-то элемента из (рис. 8.2.1):

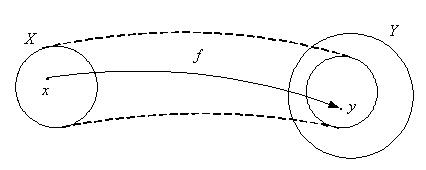
Рис. 8.2.1

Если каждый элемент из есть изображением, по крайней мере, одного элемента из , говорят, что имеет место отображение на (рис. 8.2.2):

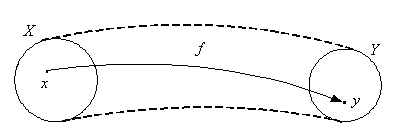
Рис. 8.2.2

Отображение числового множества во множество всех действительных чисел называется числовой функцией.

Если для любых двух различных элементов их изображения также различны, то говорят, что имеет место взаимнооднозначное отображение. Обратное отображение есть взаимно однозначное также, иначе говоря, эквивалентно . С помощью кругов Эйлера это изображается следующим образом (рис. 8.2.3):

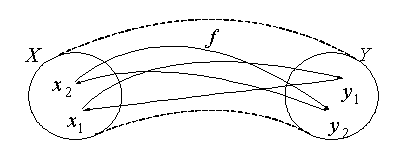
Рис. 8.2.2

Задание числовой функции предполагает не только указание закона , но и области определения функции.

Существует три основных способа задания функции.

1. Табличный способ:

			...
			...

В качестве примеров можно указать таблицы логарифмов; тригонометрические таблицы; таблицы, полученные в результате опытов.

2. Графический способ (рис. 8.2.4):

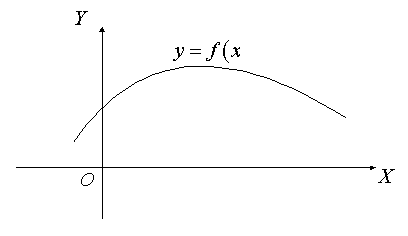
Рис. 8.2.4

График получается в результате изображения множества точек ( ) на координатной плоскости, где , а принимает значения из . Чтобы множество на плоскости было графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси , пересекала его не более чем в одной точке.

В произвольных случаях, очевидно, необходимо говорить не о двумерных пространствах, а о трехмерных и о многомерных, то есть о связи произвольного количества элементов. Однако основные определения функции не меняются.

3. Аналитический способ предполагает наличие формулы, содержащей совокупность математических операций, которые надо произвести над аргументом , чтобы получить значение функции.

К основным формам аналитического задания функции относятся:

a) явная форма задания . Например,

;

или

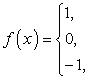
(данная функция носит название сигнум , , );

b) неявная форма задания. Функция задается в виде уравнения с двумя неизвестными , причем множество упорядоченных пар, являющихся решением данного уравнения, таково, что любому из этого множества соответствует не более одного значения .

Встречаются функции, графики которых нельзя изобразить. Примером может служить функция Дирихле:

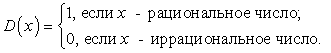
Функции обладают целым рядом свойств.

Определение 8.2.2. Функция , называется монотонно возрастающей на множестве X, если для , для которых x₁ < x₂, выполняется условие .

Аналогично определяется монотонно убывающая функция.

Определение 8.2.3. Функция , называется ограниченной снизу, если , что для выполняется условие .

Определение 8.2.4. Функция , называется ограниченной сверху, если , что для .

Определение 8.2.5. Функция , называется ограниченной, если , что для .

Определение 8.2.6. Функция называется четной, если справедливо .

График такой функции симметричен относительно оси . Пример: (рис. 8.2.5).

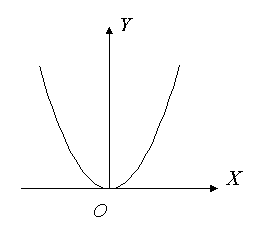
Рис. 8.2.5

Определение 8.2.7. Функция называется нечетной, если справедливо .

График нечетной функции симметричен относительно начала координат. Пример: (рис. 8.2.6).

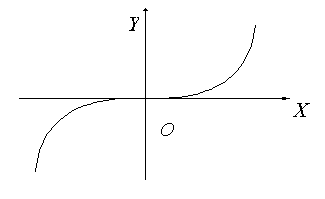
Рис. 8.2.6

Определение 8.2.8. Функция называется периодической, если , где – период функции.

Чаще всего функция имеет наименьший или основной период, остальные периоды кратны ему.

Определение 8.2.9. Пусть заданы две функции , а , причем область допустимых значений совпадает с областью определения функции , тогда каждому из области соответствует такое, что , где . Такую функцию называют сложной и записывают .

Например, .

Определение 8.2.10. Пусть задана монотонная функция , тогда обратной ей называют функцию , которая ставит каждому элементу из области значений заданной функции в соответствие все те элементы из области определения функции , для которых .

Например, и взаимно обратные функции. Графики взаимно обратных функций представляют собой одну и ту же линию. Если же переобозначить и в обратной функции, то есть , то графики будут симметричны относительно биссектрисы первого и третьего координатных углов.