Лекция 8. Раздел 8.4
Бесконечно малые величины и их свойства.

Так как на величину предела функции в точке , в случае его существования, никаких ограничений не накладывается, то этим числом может быть и ноль. Этот случай занимает особое место в теории пределов.

Определение. Функция называется бесконечно малой величиной при , если .

Точно так же вводится понятие бесконечно малой величины, если стремится к .

Из определения предела в п. 8.3 следует, что бесконечно малую величину можно охарактеризовать следующим образом.
Если , то это значит, что , то есть бесконечно малая величина это функция, которая меньше любого наперед заданного положительного числа.

Бесконечно малые величины обладают целым рядом важных свойств, на которых опираются все основополагающие понятия дифференциального и интегрального исчислений.

Теорема 8.4.1. Если при функции и являются бесконечно малыми, то их алгебраическая сумма также бесконечно малая величина при .

Доказательство. Так как и бесконечно малые величины, то по определению

,

.

Так как и могут быть разными, обозначим . Тогда, при условии , будут выполняться оба требования. Но если и могут быть меньше любого наперед заданного положительного числа, то они будут меньше и .

Обозначим . Отсюда следует, что

,

то есть является бесконечно малой величиной, что и требовалось доказать. Это правило справедливо для любого конечного числа слагаемых.

Теорема 8.4.2. Если при функция является бесконечно малой величиной, а функция – ограниченной, то их произведение есть величина бесконечно малая при .

Доказательство. Так как бесконечно малая величина, то

.

С другой стороны, если ограниченная функция, то . Поскольку может быть меньше любого наперед заданного положительного числа, то .

Обозначим . Отсюда следует, что

,

то есть является бесконечно малой величиной, что и требовалось доказать. Это правило тем более справедливо, если перемножаются бесконечно малые величины.

Для доказательства третьего свойства рассмотрим вспомогательную теорему.

Теорема 8.4.3. Если , то функция является ограниченной при .

Доказательство. Так как , то из определения предела следует, что . Отсюда,

.

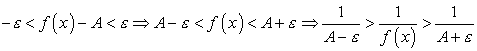Но и , и некоторые числа, значит, ограничена сверху и снизу, то есть ограниченная функция, что и требовалось доказать.

Теорема 8.4.4. Если при функция является бесконечно малой величиной, а функция в точке имеет предел, отличный от нуля, то их частное есть бесконечно малая величина.

Доказательство. Представим в виде 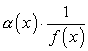. Согласно теореме 3 сомножитель – величина ограниченная, но согласно теореме 2 произведение бесконечно малой величины на ограниченную величину есть величина бесконечно малая, что и требовалось доказать.