Лекция 9. Раздел 9.3
Первый замечательный предел.
При вычислении пределов различных числовых последовательностей и функций могут быть получены различные результаты. Предел может быть равен какому-то числу, может быть равен бесконечности, может вообще отсутствовать, но самым сложным является случай, когда вместо предела получается некоторая неопределенность, например, ![]() ,
, ![]() ,
, ![]() и т.д. Существует множество неопределенностей такого типа, однако наиболее существенными из них являются две. Изучим вначале первую из них.
и т.д. Существует множество неопределенностей такого типа, однако наиболее существенными из них являются две. Изучим вначале первую из них.
Пусть дана функция ![]() . Очевидно, что она не определена при
. Очевидно, что она не определена при ![]() , так как в этом случае и числитель и знаменатель дроби обращаются в ноль. Найдем предел этой функции, когда
, так как в этом случае и числитель и знаменатель дроби обращаются в ноль. Найдем предел этой функции, когда ![]() стремится к нулю, то есть
стремится к нулю, то есть ![]() .
.
Для решения данной задачи рассмотрим окружность единичного радиуса (рис. 9.3.1).
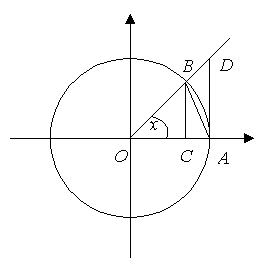
Рис. 9.3.1
Здесь ![]() – фиксированный радиус;
– фиксированный радиус; ![]() – радиус, вращающийся против часовой стрелки;
– радиус, вращающийся против часовой стрелки; ![]() ;
; ![]() – центральный угол, причем
– центральный угол, причем ![]() .
.
Соединим точки ![]() и
и ![]() хордой, из точки
хордой, из точки ![]() опустим перпендикуляр на
опустим перпендикуляр на ![]() , а из точки
, а из точки ![]() восстановим перпендикуляр до пересечения с
восстановим перпендикуляр до пересечения с ![]() .
.
Найдем вначале ![]() . На рисунке дуга
. На рисунке дуга ![]() имеет длину, равную
имеет длину, равную ![]() , а
, а 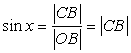 . Так как
. Так как ![]() , то
, то ![]() . Если устремить
. Если устремить ![]() к нулю, то из четвертого свойства пределов (п. 9.2) следует, что
к нулю, то из четвертого свойства пределов (п. 9.2) следует, что ![]() .
.
Найдем теперь ![]() . Так как
. Так как ![]() , то
, то
![]() .
.
Теперь перейдем к рассмотрению ![]() . Из рисунка следует, что
. Из рисунка следует, что ![]() . Здесь
. Здесь ![]() ;
; 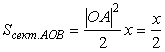 ;
; ![]() . Следовательно,
. Следовательно, ![]() . Разделим все неравенство на
. Разделим все неравенство на ![]() . Так как
. Так как ![]() , то
, то ![]() и знак неравенства при делении не изменится. Получим
и знак неравенства при делении не изменится. Получим ![]() . Переходим к обратным величинам
. Переходим к обратным величинам ![]() . Вычислим предел в данном неравенстве, что можно сделать на основании свойства 9.2.6 пределов. Так как в данном неравенстве
. Вычислим предел в данном неравенстве, что можно сделать на основании свойства 9.2.6 пределов. Так как в данном неравенстве ![]() , то на основании свойства 9.2.4 пределов
, то на основании свойства 9.2.4 пределов
![]() .
.
Это выражение и называется первым замечательным пределом.
Следствие 9.3.1. 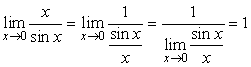 .
.
Следствие 9.3.2. ![]() .
.
Следствие 9.3.3. 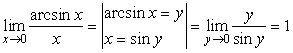 .
.
Следствие 9.3.4. 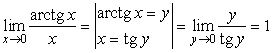 .
.
Отметим в заключение, что первый замечательный предел был получен при условии, что ![]() . Если
. Если ![]() , то
, то ![]() .
.
