Лекция 6. Раздел 6.1
Обратная матрица.

При рассмотрении действий над матрицами были введены операции сложения, вычитания, умножения матрицы на число, умножения матрицы на матрицу. Ничего не было сказано о делении на матрицу. Но такая операция фактически тоже существует. Она эквивалентна умножению на обратную матрицу. Рассмотрим, что же это такое.

Определение 6.1.1. Матрица , удовлетворяющая вместе с матрицей равенствам , где – единичная матрица, называется обратной к и обозначается .

Поскольку и обладают в произведении перестановочным свойством, то обе матрицы должны быть квадратными и одного порядка.

Прежде чем рассматривать вопрос о существовании обратной матрицы, введем некоторые понятия.

Определение 6.1.2. Если определитель квадратной матрицы отличен от нуля, то матрица называется невырожденной. В противном случае она называется вырожденной.

Определение 6.1.3. Пусть дана квадратная матрица

.

Матрицей союзной или присоединенной к матрице называется матрица

,

где алгебраические дополнения элементов данной матрицы.

Необходимо обратить внимание на то, что в матрице алгебраические дополнения к элементам -ой строки расположены в -ом столбце.

Теорема 6.1.1. Определитель произведения матриц равен произведению определителей этих матриц, то есть .

Теорема 6.1.2. Матрица имеет обратную матрицу только в том случае, если она невырожденная.

Доказательство. Пусть для матрицы существует обратная , тогда . Отсюда следует, что . Таким образом, , иначе единицы справа быть не может.

Теорема 6.1.3. У каждой невырожденной матрицы существует единственная обратная матрица .

Доказательство. Предположим, что имеет две обратные матрицы и . Тогда и . Следовательно, , откуда следует, что .

Теорема 6.1.4. У каждой невырожденной квадратной матрицы существует обратная, равная .

Докажем эту теорему, вычисляя . Очевидно, что мы должны получить при этом матрицу , элементы которой находятся по формуле

.

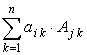В полученном выражении, если , то . Действительно, похоже на выражение для вычисления величины определителя. При этом элементы -ой строки умножаются на алгебраические дополнения -го столбца. Но так как эти дополнения содержат в себе -ую строку, то получается, что мы вычисляем определитель с двумя одинаковыми строками. Значит, он равен нулю.

Итак, если , то . Если же , то полученное выражение в точности соответствует формуле для вычисления определителя. Значит,

Но определяет диагональные элементы. Значит, в полученной матрице по главной диагонали стоят единицы, а остальные элементы – нули. Это единичная матрица . Следовательно, и , что и требовалось доказать.

Отсюда следует правило вычисления обратной матрицы:

1) находим (он должен быть не равен нулю);

2) транспонируем матрицу ;

3) заменяем каждый элемент транспонированной матрицы его алгебраическим дополнением;

4) делим каждый полученный элемент на .