Лекция 4. Раздел 4.2
Поверхности и линии первого порядка.

Определение. Линейным уравнением или уравнением первой степени, связывающим координаты точек в пространстве, называется выражение вида . В двумерном пространстве такое уравнение принимает вид .

В трехмерном пространстве это уравнение описывает некоторую поверхность, в двумерном – линию. Координаты любой точки, принадлежащей данной поверхности или линии, должны обращать уравнения в тождество.

Теорема 4.2.1. Каждое линейное уравнение в декартовой системе координат в трехмерном пространстве определяет плоскость.

Теорема 4.2.2. Каждое линейное уравнение в декартовой системе координат в двумерном пространстве определяет прямую линию.

Доказательство обеих теорем проводится совершенно одинаково, поэтому рассмотрим первую.

Уравнение поверхности в пространстве имеет вид

(4.2.1)

Как было сказано, любая точка, принадлежащая данной поверхности, должна обращать уравнение в тождество. Возьмем точку и подставим ее координаты в выражение (4.2.1), тогда оно примет вид

(4.2.2)

Вычитая из (4.2.1) выражение(4.2.2), получим:

(4.2.3)

Левую часть полученного уравнения можно рассматривать как скалярное произведение двух ортогональных векторов: и Здесь – вполне конкретный вектор, а у фиксировано только начало, а конец может оказаться в произвольной точке. При этом , так как скалярное произведение равно нулю. Множество векторов с фиксированным началом, оставаясь перпендикулярными одному и тому же вектору , образует плоскость (рис. 4.2.1). Аналогично доказывается и теорема 4.2.2.

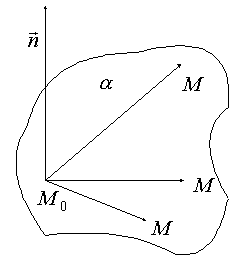
Рис. 4.2.1

Очевидно, что в уравнении плоскости , , – компоненты нормали к данной плоскости, а – характеризует расстояние от плоскости до начала координат. В уравнении прямой – компоненты нормали равны , , а – характеризует расстояние до прямой от начала координат.

Если в уравнении плоскости равен нулю один из коэффициентов , или , это значит, что нормаль ортогональна одной из осей координат. Например, в уравнении равен нулю коэффициент и или . Но если ортогонален одновременно и плоскости и оси , значит, плоскость параллельна данной оси. Если равен нулю свободный член , то плоскость проходит через начало координат.

Из доказательства теоремы 4.2.1 видно, что уравнение плоскости и прямой можно записать и в векторной форме. Для этого нужно взять скалярное произведение нормали к плоскости и одного из векторов, лежащих на ней, равным нулю, то есть . Аналогично записывается и уравнение прямой.

Уравнение плоскости можно несколько преобразовать. Учитывая, что , где и любые два вектора, лежащие на плоскости, имеем: .