Лекция 7. Раздел 7.2
Система однородных линейных алгебраических уравнений
Важное место среди всех систем линейных алгебраических уравнений занимают однородные системы с произвольными ![]() и
и ![]() :
:
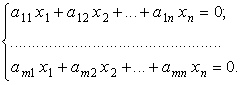
Данные системы всегда совместны, так как обязательно имеют решение вида ![]() , которое называется нулевым или тривиальным.
, которое называется нулевым или тривиальным.
Если ![]() , то, согласно теореме 7.1.1, это решение будет единственным. В частности, в случае однородной невырожденной квадратной системы ее единственное решение будет тривиальным.
, то, согласно теореме 7.1.1, это решение будет единственным. В частности, в случае однородной невырожденной квадратной системы ее единственное решение будет тривиальным.
В случае, когда ранг матрицы системы меньше числа неизвестных, то решений, согласно теореме 7.1.2, будет бесконечное множество. Пусть в этом случае матрицы - столбцы ![]() ,
, ![]() ,...,
,..., ![]() являются некоторыми решениями системы:
являются некоторыми решениями системы:
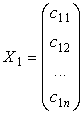 ,
, 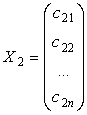 ,...,
,..., 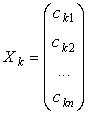 .
.
Тогда выражение ![]() будет называться их линейной комбинацией. Очевидно, что можно ввести понятие линейно зависимой и линейно независимой системы этих решений. Необходимо иметь в виду, что линейная комбинация решений системы линейных алгебраических уравнений также будет ее решением. Действительно,
будет называться их линейной комбинацией. Очевидно, что можно ввести понятие линейно зависимой и линейно независимой системы этих решений. Необходимо иметь в виду, что линейная комбинация решений системы линейных алгебраических уравнений также будет ее решением. Действительно,
Теорема. Если ранг матрицы однородной системы линейных алгебраических уравнений меньше числа неизвестных, то есть ![]() , то существует
, то существует ![]() линейно независимых решений системы
линейно независимых решений системы ![]() ,
, ![]() ,...,
,..., ![]() , а любые другие решения можно представить как их линейную комбинацию.
, а любые другие решения можно представить как их линейную комбинацию.
Доказательство. Пусть ранг основной матрицы системы ![]() . Тогда базисными неизвестными будут
. Тогда базисными неизвестными будут ![]() , а остальные
, а остальные ![]() неизвестных будут свободными. В этом случае произвольное решение системы можно записать в виде:
неизвестных будут свободными. В этом случае произвольное решение системы можно записать в виде:
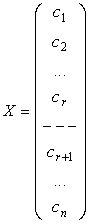 .
.
Здесь ![]() – произвольные числа, а
– произвольные числа, а ![]() однозначно определяются из системы для выбранных
однозначно определяются из системы для выбранных ![]() .
.
Рассмотрим ![]() следующих решений системы:
следующих решений системы:
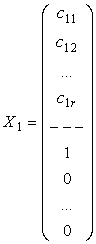 ,
, 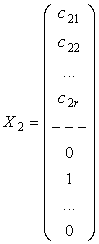 ,...,
,..., 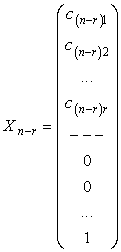 .
.
По аналогии с результатом п. 6.3 все они линейно независимы, и произвольное решение системы можно представить в виде:
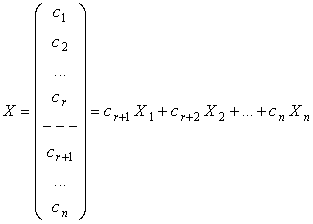 ,
,
что и требовалось доказать.
Определение. Фундаментальной системой решений однородной системы линейных алгебраических уравнений называется совокупность всех ее линейно независимых решений.
Если в фундаментальной системе решений свободные неизвестные по очереди выражаются через единицу, в то время как остальные равны нулю, то такая фундаментальная система решений называется нормированной.
