Лекция 1.Раздел 1.2
Простейшие
операции над векторами
К простейшим операциям над векторами относится сложение и вычитание векторов и умножение вектора на скаляр. Все эти операции называются линейными.
1. Сложение векторов
Определение 1.2.1Чтобы найти сумму двух векторов 
и 
необходимо конец вектора совместить с началом . Вектор 
, соединяющий точки 
и 
, будет их суммой (рис. 1.2.1).
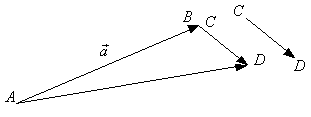Рис.
1.2.1
Обозначается сума следующим образом: 
(рис. 1.2.1). Величину
ее можно найти и другим способом. Начала
векторов и совмещаются и на них как на сторонах строится параллелограмм. Диагональ параллелограмма и будет суммой векторов (рис. 1.2.2).
Из правила параллелограмма видно, что
сумма векторов обладает переместительным
свойством 
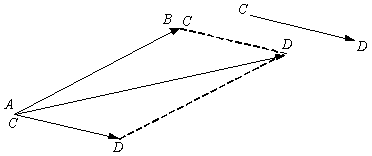Рис. 1.2.2.
Если слагаемых больше, например, три: 
, поступают следующим образом. Строят
вначале сумму 
, а затем, прибавляя 
, получают вектор 
(рис. 1.2.3).
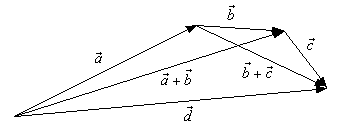Рис. 1.2.3
Из рис. 1.2.3 видно, что тот же результат будет, если сложить вначале 
, а затем прибавить 
, то есть сумма векторов обладает сочетательным свойством:
Если при сложении нескольких векторов конец последнего совпадает с началом первого, то сумма равна ноль вектору 
. Очевидно, 
.
2. Разность векторов.
Определение 1.2.2. Разностью двух векторов и 
называется такой вектор 
, сумма которого с вычитаемым дает вектор .
Значит, если , то 
.
Из определения суммы двух векторов вытекает правило построения разности. Откладываем из общей точки векторы и . Вектор соединяет концы векторов и и направлен от вычитаемого к уменьшаемому (рис. 1.2.4).
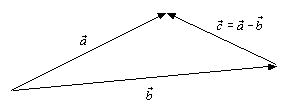Рис. 1.2.4
Видно, что если на векторах и построить параллелограмм, то одна его диагональ соответствует их сумме, а вторая – разности.
3. Умножение вектора на число.
Определение 1.2.3. Произведением вектора на число 
называется вектор , определенный следующими условиями:
1) 
;
2) вектор коллинеарен вектору ;
3) векторы и направлены одинаково, если 
, и противоположно, если 
.
Очевидно, что операция умножения вектора на число приводит к его растяжению или сжатию. Противоположный вектор 
можно рассматривать как результат умножения вектора на 
. Отсюда, 
.
Из построения параллелограмма легко убедиться, что умножение вектора на число обладает распределительным свойством:
;
и сочетательным свойством .
Из определения 1.2.3 следует, что если 
, то векторы и коллинеарны. Отсюда вытекает определение коллинеарности векторов.
Определение 1.2.4. Любые два вектора и коллинеарны, если связаны соотношением , где –некоторое число.
Величину можно определить из отношения 
. Оно положительно, если векторы направлены в одну сторону, и наоборот отрицательно, если направление векторов противоположно.
Определение 1.2.5. Вектор, длина которого равна единице, называется единичным вектором или ортом.
Обозначаются единичные векторы символами 
или 
.
Используя понятие единичного вектора, любой вектор можно представить следующим образом: 
.
