Лекция 1.Раздел 1.6
Декартовая система координат

Если в пространстве зафиксировать точку О и рассмотреть произвольную точку М, то вектор  будет называться радиус-вектором точки М относительно точки О. Если с точкой О связать еще и некоторый базис, то точке М можно сопоставить упорядоченную тройку чисел – координат ее радиус-вектора.

Определение 1.6.1. Декартовой системой координат в пространстве называется совокупность точки и связанного с ней базиса.

Точка носит название начала координат. Прямые, проходящие через начало координат в направлении базисных векторов, – осями координат. Первая называется осью абсцисс, вторая – осью ординат, третья – осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.

Определение 1.6.2. Компоненты радиус-вектора точки М по отношению к началу координат называются координатами точки М в данной системе координат.

Записывается это так: . Очевидно, в заданной системе координат упорядоченная тройка координат единственным образом определяет положение точки в пространстве.

Теорема. Чтобы найти координаты вектора, нужно из координат его конца вычесть координаты его начала.

Доказательство. Рассмотрим систему координат и две точки A и B (рис. 1.6.1).

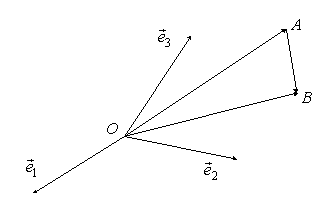Рис. 1.6.1

Их координаты , . Очевидно, . При вычитании векторов их координаты вычитаются. Значит , что и требовалось доказать.

Определение 1.6.3. Базис называется ортонормированным, если его векторы попарно ортогональны, а по длине равны единице. Декартовая система координат, при этом, называется прямоугольной системой координат.

С этой системой координат мы в дальнейшем и будем иметь дело. Ее базисные векторы обозначаются   , , .

Необходимо отметить, что тройка базисных векторов может быть пронумерована двумя способами и можно получить при этом правую и левую систему координат.

Определение 1.6.4. Упорядоченная тройка ортонормированных векторов называется правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройка векторов называется левой (рис. 1.6.2).

Рис. 1.6.2

Зная проекции вектора  , можно легко найти выражение для модуля вектора. Так как при разложении по прямоугольному базису, вектор  является диагональю параллелепипеда, то  , откуда  . На плоскости .

В пространстве направление вектора можно задать углами   , ,, которые вектор образует с осями координат. Косинусы этих углов называются направляющими косинусами вектора (рис. 1.6.3).

Пользуясь формулами для проекции вектора на ось, получаем:

    (1.6.1)

Отсюда

    (1.6.2)

Подставляя в (1.6.2) , легко получить  .

Из правила умножения вектора, заданного своими координатами, на число сразу вытекает способ проверки коллинеарности двух векторов. Действительно, если   , то   , то есть  ,  ,  . Отсюда следует, что .

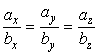Рис. 1.6.3