Лекция 1.Раздел 1.3
Проекция вектора на ось
В процессе выполнения простейших операций иногда приходится сталкиваться с таким понятием, как проекция вектора на какую-либо ось. Введем вначале понятие угла между векторами.
Определение 1.3.1. Углом между векторами 
и 
называется наименьший угол 
, на который надо повернуть один из векторов до совмещения со вторым (рис. 1.3.1)
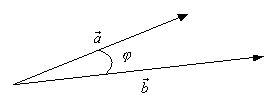(рис. 1.3.1)
Положительным считается отсчет угла против часовой стрелки.
Пусть необходимо найти проекцию вектора 
на ось 
(рис. 1.3.2). Выберем на оси начало отсчета 0 и масштаб. Совместим с началом отсчета единичный вектор 
. Тогда угол между и осью будет равен углу между и . Проецируем начало и конец вектора на ось . Тогда длина отрезка 
, а 
. Длина же проекции вектора :
Рис.
1.3.2
Определение 1.3.2. Проекцией вектора на ось называется разность между координатами проекций конца и начала вектора на ось
Очевидно, что если – острый угол, проекция положительна; если – тупой угол, то отрицательна; если 
, то проекция равна нулю.
Теорема 1.3.1. Проекция вектора на ось равна произведению модуля этого вектора на косинус угла между ними:
Доказательство теоремы вытекает из рис. 1.3.2.
Теорема 1.3.2. Проекция суммы двух векторов на ось равна сумме проекций слагаемых векторов на ту же ось.
Доказательство. Пусть 
. Обозначим проекцию точки 
через 
, точки 
– через 
, точки 
– через 
(рис. 1.3.3).
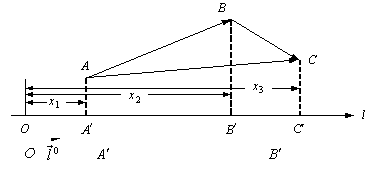Рис.
1.3.3
Тогда 
; 
; 
. Но
Теорема 1.3.3. Если вектор умножить на число 
, то его проекция на ось умножится на то же число.
Докажем для случая 
:
Если 
, то
