Лекция 1.Раздел 1.5
Базис, координаты вектора

В предыдущем параграфе было показано, что если векторы линейно зависимы, то один из них всегда можно выразить через остальные. Это приводит к мысли, что можно выбрать какую-нибудь стандартную систему векторов и тогда любой вектор можно выражать, то есть описывать, с помощью этой стандартной системы. Будут лишь меняться коэффициенты в линейных комбинациях.

Оказывается, что в плоском случае и в трехмерном случае такие стандартные системы различны.

Теорема 1.5.1. Базисом на плоскости являются два любых неколлинеарных вектора   и  , взятых в определенном порядке. Любой компланарный с ними вектор  единственным образом раскладывается по ним.

Доказательство. Возьмем два неколлинеарных вектора   и  и вектор   . Поместим их начала в одну точку (рис. 1.5.1). Проведя из конца   линии до пересечения с прямыми, на которых лежат вектора   и  , получим параллелограмм. Но тогда  можно рассматривать как сумму  и  , то есть  , что и требовалось доказать. Из этой теоремы видно, что любые три компланарных вектора линейно зависимы (на основании теоремы 1.4.2), а два – нет, если они не коллинеарны.

Здесь числа  , называются аффинными координатами вектора  на плоскости в базисе    ,  . Записывается это так: .

Теорема 1.5.2. Базисом в пространстве являются три любых некомпланарных вектора   ,  , , взятых в определенном порядке. Любой вектор единственным образом раскладывается по ним.

Рис. 1.5.1

Возьмем три некомпланарных вектора   ,  , и вектор  . Совместим их начала (рис. 1.5.2).

Рис. 1.5.2

Из конца  поведем прямую, параллельную  , до пересечения с плоскостью, где лежат    и   ,. Вектор , согласно теореме 1, можно представить в виде:  . Но, с другой стороны ,, что и требовалось доказать. Значит, в трехмерном пространстве любые четыре вектора линейно зависимы, а три – нет.

Числа , , называются аффинными координатами вектора в базисе   ,  , , то есть  .

Очевидно, любым заданным координатам при помощи базиса можно поставить в соответствие единственный вектор. Но тогда сложение векторов, заданных координатами, и умножение векторов на число удобно представить через их координаты. Действительно,

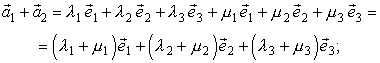    (1.5.1)

    (1.5.2)