Лекция 1.Раздел 1.4
Линейная зависимость векторов

Определение 1.4.1. Векторы   ,  ,..., называются линейно зависимыми, если существуют такие числа  , ,... не все равные нулю, для которых имеет место равенство .

Пример. Сумма трех или двух векторов на плоскости.

Определение 1.4.2. Векторы ,  ,..., называются линейно независимыми, если равенство имеет место только при  .

Определение 1.4.3. Выражение называется линейной комбинацией векторов ,  ,..., .

Теорема 1.4.1. Если векторы ,  ,..., линейно зависимы, то один из них всегда можно представить в виде линейной комбинации остальных.

Доказательство. Если векторы ,  ,..., линейно зависимы, то из определения 1 следует, что . Пусть , тогда  и 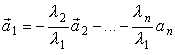 , что и требовалось доказать.

Теорема 1.4.2. Если один из векторов представлен в виде линейной комбинации остальных, то все эти векторы линейно зависимы.

Доказательство. Пусть 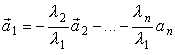  . Перенося все в одну сторону, получим  . Так как здесь, по крайней мере, при  коэффициент не равен нулю, то из определения 1 следует, что векторы линейно зависимы.